THE FINER DETAILS
Firstly, the question of exact size of the pyramid should be answered. Petrie's survey and notes identify three separate measurements for the base side-lengths: the core blocks; the casing; specific points within the sockets. We can accept that the core blocks form the structure of the pyramid and the casing blocks were masoned to show the smooth angle of the pyramid, while the sockets were placed at the four corners and each corner had a different depth, but mainly they allowed for the corner casing blocks to rest beneath the pavement level and ritually housed offerings of some kind beneath these corner blocks. Petrie states that while all manner of deduction can precisely estimate the true measurements as coming from what is observed, there is the potential for slight discrepancies in the direct observations that affect the whole, not only through estimation of projections of positions and angles but also through the accumulation of slight errors in the performance of the survey. An example is the approach to the position of the original casing: in one respect, remains in-situ can certainly give credence to particulars of a side of the pyramid, and also the form of the pavement where the extent of a casing block can be identified as having had its position, but it can be difficult to estimate the exact corner of the pyramid when the casing blocks are no longer there unless the edges of two sides are projected through to their intersection. This is a course of 'best fit' scenario. Petrie was fastidious with alignments, projections and estimations when destruction had removed the very matter of an object, and we cannot help but acknowledge from his own words that even still, slight errors can exist.
The particulars of the forms of the sockets indicate that the casing blocks angled down into the pavement level and did not meet their base sides exactly but were possibly up to 4" inside the edges of the sockets. Petrie was able to show this from calculations of the angle of the proposed casing at the corners, having deduced this from both existing casing blocks and also projections down at those locations using straight edges and measurements to accommodate the projections.
It is a little harder to take a similar approach to the core blocks due to the weathering upon them or missing blocks at the corners, so introducing an average of casing thickness upon the whole and then defining the lengths of the sides could do; but Petrie was able to give what he considered to be very good estimations to the size of the pyramid by approaching measurements and angles in mathematically precise ways according to direct observations and projections associated with those observations.
For the base of the pyramid, Petrie used the precise locations of the corners of the core blocks and the exact forms of the sockets, and estimated the four sides that included the casing, and while there was very little difference between all sides, he defined an average to them of 9,068.8" in length. To verify whether this is exact enough for this analysis, the wonder at the height of the pyramid will have to be acknowledged, and Petrie certainly had his work cut out for him due to the top-most courses of it missing. From observations of the angle of the pyramid's sides without the casing, and measurements upon what exists at the top, he was able to compute a small range for the true height at between 5,769" and 5,783", with his best estimate of 5,776" as the more likely height.
There has been much speculation that the pyramid, with its base and its height, are related through pi, indicating the properties of a circle. To find the circumference of a circle, we take the radius measurement of it and multiply it by 2 to define its diameter, and multiply by pi to find the measurement of its circumference. For the pyramid, the estimation of pi is supposedly exhibited in the height of it in relation to the perimeter of its base: (9068.8" x 4) / pi / 2 = 5,773.3774" approximately.
If the height of 5,776" is to be appreciated in relation to the radius of a circle to its circumference, then the average of the side length would have to be approximately 9,072.9196", and slightly less or more if the range of 5,769" to 5,783" is judged. These are the slight differences that can be observed and are associated to pi being exact rather than a very close estimation due to a fraction being had, such as has been proposed by the use of 22/7 as being used by the ancient Egyptians. For this estimate, the resulting height would be approximately 5,771.0545" for a side length of 9,068.8".
As much as possible, the exactness of this analysis relies upon true measurements and angles, and just for the size of the pyramid there are already small variations to what measurements and angles are to be used which could introduce a range of potentials upon the whole. It is okay to have a small range, as the truth to the exactness would eventually be uncovered, but it is better to try and identify the exactness in the outset if at all possible. While there has been some speculation whether pi was known let alone used in the pyramid's planning and construction, already the figures do allude to it, and one further identification of a measurement of the pyramid can confirm that pi's exact figure was known and used, and this is identified in the Grand Gallery.
Petrie states the sloping length of the roof of the gallery is approximately 1,838.6" in its entirety, and this figure multiplied by pi gives us approximately 5,776.13225". To use 22/7 for pi, the formula would see a height of 5,778.45714", and certainly within the range proposed by Petrie. As the gallery is a measurement within the pyramid and not of its outside, and the form of it is solid and bereft of any destruction to it like the King Chamber has suffered, so too the outside of the pyramid, it is quite a direct comparison to the size that it should not be overlooked as being important.
Another possibility that can be considered in regards to the height and side lengths is direct interaction between the height and half the length which, in a simple attribute of rise over run, the ancient Egyptians defined a term for use in construction techniques called the seked. The seked is a simple formula that allows for the angle or slope of the hypotenuse of a right angled triangle to be known, based upon rise over run, or the height in relation to the base length. This formula relies upon the identities of the Royal Cubit, palm and digit as units of measurement, and also the resulting interaction of them expressed as the seked, or the gradient in our term.
As much as can be known, a Royal Cubit is composed of 7 palms, and 1 palm is composed of 4 digits. For the Great Pyramid, it is said to have a seked of 5 palms, 2 digits, expressed from an assertion that there are 280 cubits in height and 220 cubits as the half base-length. The identification of a seked is such that the steeper the gradient, the lower the seked, while the lower the gradient equates to a higher seked. As Petrie has estimated that a Royal Cubit equals approximately 20.632”, this means a height of 5,776.96”, with a base-length of 9,078.08”, but this length is a little big when associated to Petrie's measurements. This seked amount sees an angle of 51º 50' 24”, which is possible for the angle of the pyramid, but for the most part does not fit exactly according to the findings of Petrie.
The seked is defined by taking the height of 1 Royal Cubit where the hypotenuse meets the base of the triangle, then measuring back to the hypotenuse from the upright. It is possible that the closest estimation for the seked has been used for the description of the pyramid, or that the length of a base-side of the pyramid has been under-measured. Of course there may be some undefined property that is associated with the seked in regards to the pyramid that we have not become aware of yet; or the slope of the pyramid is truly based upon some other aspect instead of the seked, but is used to identify the slope to the easiest of mathematical associations, whether it is exact or not, much like pi having a close fraction of 22/7. Of course, having the gallery roof length does allude to a very good description of pi towards the construction, otherwise it is a very grand coincidence.
One other possibility could be the Golden Mean, or phi, with an approximate numerical expression of 1.61803398875. This factor is associated with measurement and formally expressed as a ratio upon a straight line which has been divided into two lengths, the one length can be considered as 1 unit, and the other length considered as 1.61803398875 units; the second length can then be considered as 1 unit while the entire length of the line undivided is considered as 1.61803398875 units. It is a neat numerical association which has as its basis a simple formula: ( sq.root5 + 1) / 2. The part of having this associated with the side-length of the pyramid is the square root of phi, equalling approximately 1.272. With the interaction between the height of the pyramid and the square root of phi, a figure of approximately 9,081.62 is found, which is 12.8” longer than Petrie's survey defines for the side length; or about 2.5” more than the complete length when the seked is accepted.
For the height, the association could also be based upon a factor of the square root of 3 which also has its own hierarchy of number. The reciprocal of this square root is 0.57735, and times by 10,000 = the pyramid's height of 5773.5”. Squared = 0.3333repeat; squared again = 0.1111repeat; and squared once more = 0.0123456790123456790repeat. This last figure is noticeable for missing the 8. Including the zero, it is a number of nine figures repeating, and may have a further relevance according to simple number play which is beyond the scope of this presentation to include.
With several potential formulas for associating the height of the pyramid to the length of a side at its base, one in particular will be used and this comes from the roof of the gallery with pi. As such, the model will identify the true height of the pyramid as approximately 5,776" with an average side length of 9,073". In using it though, it will define a true angle of the casing as approximately 51.854 degrees, or 51º 51' 14.4", and this angle is certainly tolerable according to Petrie's own measurements and estimations, which had 51º 52' with plus or minus 2' as an average for the four sides, including observations that some casing stones on the north side exhibited an angle of 51º 46' 45", and according to the mouth of the southern shaft coming from the King Chamber, the south side could have been as much as 51º 57' 30". It should be noted that in one observation of the probable angle, Petrie identified the seked of 2 over pi, which does give the exact angle of 51º 51' 14", but he does not offer the length of 9,073” for the height of 5,776” to equate to it, nor a better height when 9,068.9968” is used for the side-length.
Having four separate depths to the sockets, and four separate lengths to each side, it is not unreasonable that each side had a separate angle to it also, and rather than speculate that these are due to either the accumulated differences of the construction itself, or for specific inclusions from either ritualistic or directly planned matters, they can be overlooked in the outset of the analysis in the understanding that they exist and might be identified as to why at some stage. Further, because of the possible associations to do with different factors contributing to the side-lengths of the pyramid, even for those that are yet to be speculated upon that may relate to a representation of the size of earth itself being associated with the size of the pyramid – as has been offered up by other investigations into the pyramid – the possibility of the differing depths of the sockets may have something to uncover, and these will be questioned at some point in the analysis.
As the matter of the pyramid's size has been dealt with, and Petrie has so meticulously measured all the features within it and given definite figures as well as estimations of errors, the question of the shafts within the King and Queen Chambers should be addressed as there are slight discrepancies and problems associated with defining them within the pyramid.
Petrie describes the shafts of the Queen Chamber as rising into the pyramid after their short, horizontal straight lengths from within the chamber, at angles:
North Channel being an average of 37.4667º, where the western side of the shaft at first bend is 37.55º; middle of shaft is 37.4267º; eastern side of shaft is 37.4167º.
There can only be speculation as to why Petrie uses 37.4667º as the mean, considering 37.4833º would have been the mean.
South Channel being an average of 38.4667º, where western side is 38.4667º; middle is 38.33º; eastern side as 38.5833º.
Gantenbrink's Upuaut and the subsequent Upuaut 2 used in the shafts were able to survey the entirety of the shafts, and gave angles for them at their various bends throughout. The results for the south shaft are 39.6078º for its entire length of approximately 2,275" from the first bend once it leaves the chamber to its blocked end. The difference between the south shaft by both observations is 1.1411 degrees. A little more than one degree could have quite an effect upon the results of the analysis.
For the north shaft, Upuaut defined several angles to the shaft as it left the chamber and bent around the proximity of the gallery, but Gantenbrink provided nothing definite about where these angles lay within the shaft. Having a range between 33.3º and 40.1º could place the shaft anywhere on its rise through the pyramid, and as there is a difference between the two men for the south shaft, there could also be a difference between them for the first bend of the north shaft. According to Gantenbrink's diagrams of the shafts, the first angle is approximately 43º which is not included in his 'range'. There is another way to determine the north shaft, and that is by looking at the shafts of the King Chamber firstly.
Assessing the measurements for the King Chamber south shaft, we find Petrie has these, being taken from the outside down the shaft, and he does not have any angles from within the chamber:
At 0 to 120” from the surface: 45.4183º
At 120 to 240”: 45.5019º
At 240 to 360”: 45.4325º
At 360 to 480”: 45.4206º
At 480 to 600”: 45.2553º
At 600 to 720”: 45.1283º
At 720 to 840”: 44.4383º
Mean: 45.2278º as stated by Petrie, although the mean should be taken as 44.9701º.
Gantenbrink has the following observations, from inside the pyramid going outwards:
Start of bend: 39.2º
Next bend: 50.54º
Final bend and full length to exit: 45º
Gantenbrink provides the distance from within the chamber to the first bend, and with the angle there plus measurements and angles for the next bends and lengths, these can be modelled and laid out. Petrie states the position of the exit point upon the pyramid casing as being 3,148.95” above the pavement, in the 104th course if this were levelled out to the casing. Taking Gantenbrink’s figures places the exit point some 40-odd inches above the actual exit point, and this cannot do for the model’s exactness, let alone the pyramid itself. In using Gantenbrink’s initial angles and lengths of the shaft between these angles, the final angle leading to the casing would be 43.665º, not 45º. To use Petrie’s angles down to the 840” mark would mean an angle of 42º from that to Gantenbrink’s third angle, which is 3º difference. One possibility is to take the first bend beyond the chamber and link it to the exit point upon the proposed casing, and accept a complete angle of 44.052º, no matter the adjustments through the shaft itself. This can be called a 'true angle', and true angles could be applied to all the shafts in lieu of the various angles they contain.
For the north shaft, Petrie has measured from the outside coming down the shaft:
At 84 to 180": 32.079º
At 180 to 300": 31.621º
At 300 to 372": 30.721º
Mean: 31.55º as stated by Petrie, but the mean should be 31.4º.
Gantenbrink has more detailed angles going up the shaft, starting with the first angle after leaving the chamber at 17º, and after bending several times around the proximity of the gallery, ending with 32.6º for the last length to the exit. This is half a degree more than Petrie has for the final part of the shaft, and modelling this in the pyramid causes a problem with the exit upon the casing being some 60-odd inches above its actual exit point. Petrie has the measurement of 3,119.85” above the pavement for the exit point, being the base of the 103rd course if it were extended out to the casing. In consideration of the exit point upon the casing, the angle of 30.718º must be correct instead of 32.6º for the entire last length, despite what slight changes must exist.
Considering the north shaft of the Queen Chamber, and that there are several adjustments to the shaft going around the gallery, the most plausible operation is to consider the south shaft, and correct the angles appropriately towards an acceptable result. Final adjustments can be made once the correct astral overlay is found, and the true angles of the shafts can be understood. By choosing 'true angles', the better estimation for them would be to take the first bend in the shafts after they have left the chambers, and the end-positions of the shafts themselves, and define the angles they reveal.
For the King Chamber shafts, as we know their exit points upon the surface of the pyramid and the locations of the first bends from the chamber, the 'true angles' can be given as:
South shaft: 44.052º
North shaft: 30.945º
For the Queen Chamber shafts:
South shaft: 39.415º
North shaft: 40.2º
Again, these will rely on the correct astronomical overlay to confirm them, but certainly they will suffice despite the arguments for using the angles of either men implicitly.
The angle of the entrance passage - that which enters the pyramid and reaches the lower passage to the subterranean chamber - is 26.523º. The angle of the ascending passage - that which extends from the blocking plugs leading to the Grand Gallery - is 26.042º. For the Gallery itself, an angle of 26.278º is identified, and these angles are given by Petrie. The floor levels of the three chambers and their passages are from Petrie.
With these particulars, the model was constructed and accounted for with projections to the shaft angles and passage angles leading away from the pyramid; intersections were identified according to the heights of the shafts and passages and the potential of exacting intersection they had with each other, and also with extended alignments from such as floor levels. The following image is the reconstructed pyramid with projections of passages, shafts, and the floor levels of the two upper chambers, and floor and ceiling levels of the passage to the Subterranean Chamber.
Firstly, the question of exact size of the pyramid should be answered. Petrie's survey and notes identify three separate measurements for the base side-lengths: the core blocks; the casing; specific points within the sockets. We can accept that the core blocks form the structure of the pyramid and the casing blocks were masoned to show the smooth angle of the pyramid, while the sockets were placed at the four corners and each corner had a different depth, but mainly they allowed for the corner casing blocks to rest beneath the pavement level and ritually housed offerings of some kind beneath these corner blocks. Petrie states that while all manner of deduction can precisely estimate the true measurements as coming from what is observed, there is the potential for slight discrepancies in the direct observations that affect the whole, not only through estimation of projections of positions and angles but also through the accumulation of slight errors in the performance of the survey. An example is the approach to the position of the original casing: in one respect, remains in-situ can certainly give credence to particulars of a side of the pyramid, and also the form of the pavement where the extent of a casing block can be identified as having had its position, but it can be difficult to estimate the exact corner of the pyramid when the casing blocks are no longer there unless the edges of two sides are projected through to their intersection. This is a course of 'best fit' scenario. Petrie was fastidious with alignments, projections and estimations when destruction had removed the very matter of an object, and we cannot help but acknowledge from his own words that even still, slight errors can exist.
The particulars of the forms of the sockets indicate that the casing blocks angled down into the pavement level and did not meet their base sides exactly but were possibly up to 4" inside the edges of the sockets. Petrie was able to show this from calculations of the angle of the proposed casing at the corners, having deduced this from both existing casing blocks and also projections down at those locations using straight edges and measurements to accommodate the projections.
It is a little harder to take a similar approach to the core blocks due to the weathering upon them or missing blocks at the corners, so introducing an average of casing thickness upon the whole and then defining the lengths of the sides could do; but Petrie was able to give what he considered to be very good estimations to the size of the pyramid by approaching measurements and angles in mathematically precise ways according to direct observations and projections associated with those observations.
For the base of the pyramid, Petrie used the precise locations of the corners of the core blocks and the exact forms of the sockets, and estimated the four sides that included the casing, and while there was very little difference between all sides, he defined an average to them of 9,068.8" in length. To verify whether this is exact enough for this analysis, the wonder at the height of the pyramid will have to be acknowledged, and Petrie certainly had his work cut out for him due to the top-most courses of it missing. From observations of the angle of the pyramid's sides without the casing, and measurements upon what exists at the top, he was able to compute a small range for the true height at between 5,769" and 5,783", with his best estimate of 5,776" as the more likely height.
There has been much speculation that the pyramid, with its base and its height, are related through pi, indicating the properties of a circle. To find the circumference of a circle, we take the radius measurement of it and multiply it by 2 to define its diameter, and multiply by pi to find the measurement of its circumference. For the pyramid, the estimation of pi is supposedly exhibited in the height of it in relation to the perimeter of its base: (9068.8" x 4) / pi / 2 = 5,773.3774" approximately.
If the height of 5,776" is to be appreciated in relation to the radius of a circle to its circumference, then the average of the side length would have to be approximately 9,072.9196", and slightly less or more if the range of 5,769" to 5,783" is judged. These are the slight differences that can be observed and are associated to pi being exact rather than a very close estimation due to a fraction being had, such as has been proposed by the use of 22/7 as being used by the ancient Egyptians. For this estimate, the resulting height would be approximately 5,771.0545" for a side length of 9,068.8".
As much as possible, the exactness of this analysis relies upon true measurements and angles, and just for the size of the pyramid there are already small variations to what measurements and angles are to be used which could introduce a range of potentials upon the whole. It is okay to have a small range, as the truth to the exactness would eventually be uncovered, but it is better to try and identify the exactness in the outset if at all possible. While there has been some speculation whether pi was known let alone used in the pyramid's planning and construction, already the figures do allude to it, and one further identification of a measurement of the pyramid can confirm that pi's exact figure was known and used, and this is identified in the Grand Gallery.
Petrie states the sloping length of the roof of the gallery is approximately 1,838.6" in its entirety, and this figure multiplied by pi gives us approximately 5,776.13225". To use 22/7 for pi, the formula would see a height of 5,778.45714", and certainly within the range proposed by Petrie. As the gallery is a measurement within the pyramid and not of its outside, and the form of it is solid and bereft of any destruction to it like the King Chamber has suffered, so too the outside of the pyramid, it is quite a direct comparison to the size that it should not be overlooked as being important.
Another possibility that can be considered in regards to the height and side lengths is direct interaction between the height and half the length which, in a simple attribute of rise over run, the ancient Egyptians defined a term for use in construction techniques called the seked. The seked is a simple formula that allows for the angle or slope of the hypotenuse of a right angled triangle to be known, based upon rise over run, or the height in relation to the base length. This formula relies upon the identities of the Royal Cubit, palm and digit as units of measurement, and also the resulting interaction of them expressed as the seked, or the gradient in our term.
As much as can be known, a Royal Cubit is composed of 7 palms, and 1 palm is composed of 4 digits. For the Great Pyramid, it is said to have a seked of 5 palms, 2 digits, expressed from an assertion that there are 280 cubits in height and 220 cubits as the half base-length. The identification of a seked is such that the steeper the gradient, the lower the seked, while the lower the gradient equates to a higher seked. As Petrie has estimated that a Royal Cubit equals approximately 20.632”, this means a height of 5,776.96”, with a base-length of 9,078.08”, but this length is a little big when associated to Petrie's measurements. This seked amount sees an angle of 51º 50' 24”, which is possible for the angle of the pyramid, but for the most part does not fit exactly according to the findings of Petrie.
The seked is defined by taking the height of 1 Royal Cubit where the hypotenuse meets the base of the triangle, then measuring back to the hypotenuse from the upright. It is possible that the closest estimation for the seked has been used for the description of the pyramid, or that the length of a base-side of the pyramid has been under-measured. Of course there may be some undefined property that is associated with the seked in regards to the pyramid that we have not become aware of yet; or the slope of the pyramid is truly based upon some other aspect instead of the seked, but is used to identify the slope to the easiest of mathematical associations, whether it is exact or not, much like pi having a close fraction of 22/7. Of course, having the gallery roof length does allude to a very good description of pi towards the construction, otherwise it is a very grand coincidence.
One other possibility could be the Golden Mean, or phi, with an approximate numerical expression of 1.61803398875. This factor is associated with measurement and formally expressed as a ratio upon a straight line which has been divided into two lengths, the one length can be considered as 1 unit, and the other length considered as 1.61803398875 units; the second length can then be considered as 1 unit while the entire length of the line undivided is considered as 1.61803398875 units. It is a neat numerical association which has as its basis a simple formula: ( sq.root5 + 1) / 2. The part of having this associated with the side-length of the pyramid is the square root of phi, equalling approximately 1.272. With the interaction between the height of the pyramid and the square root of phi, a figure of approximately 9,081.62 is found, which is 12.8” longer than Petrie's survey defines for the side length; or about 2.5” more than the complete length when the seked is accepted.
For the height, the association could also be based upon a factor of the square root of 3 which also has its own hierarchy of number. The reciprocal of this square root is 0.57735, and times by 10,000 = the pyramid's height of 5773.5”. Squared = 0.3333repeat; squared again = 0.1111repeat; and squared once more = 0.0123456790123456790repeat. This last figure is noticeable for missing the 8. Including the zero, it is a number of nine figures repeating, and may have a further relevance according to simple number play which is beyond the scope of this presentation to include.
With several potential formulas for associating the height of the pyramid to the length of a side at its base, one in particular will be used and this comes from the roof of the gallery with pi. As such, the model will identify the true height of the pyramid as approximately 5,776" with an average side length of 9,073". In using it though, it will define a true angle of the casing as approximately 51.854 degrees, or 51º 51' 14.4", and this angle is certainly tolerable according to Petrie's own measurements and estimations, which had 51º 52' with plus or minus 2' as an average for the four sides, including observations that some casing stones on the north side exhibited an angle of 51º 46' 45", and according to the mouth of the southern shaft coming from the King Chamber, the south side could have been as much as 51º 57' 30". It should be noted that in one observation of the probable angle, Petrie identified the seked of 2 over pi, which does give the exact angle of 51º 51' 14", but he does not offer the length of 9,073” for the height of 5,776” to equate to it, nor a better height when 9,068.9968” is used for the side-length.
Having four separate depths to the sockets, and four separate lengths to each side, it is not unreasonable that each side had a separate angle to it also, and rather than speculate that these are due to either the accumulated differences of the construction itself, or for specific inclusions from either ritualistic or directly planned matters, they can be overlooked in the outset of the analysis in the understanding that they exist and might be identified as to why at some stage. Further, because of the possible associations to do with different factors contributing to the side-lengths of the pyramid, even for those that are yet to be speculated upon that may relate to a representation of the size of earth itself being associated with the size of the pyramid – as has been offered up by other investigations into the pyramid – the possibility of the differing depths of the sockets may have something to uncover, and these will be questioned at some point in the analysis.
As the matter of the pyramid's size has been dealt with, and Petrie has so meticulously measured all the features within it and given definite figures as well as estimations of errors, the question of the shafts within the King and Queen Chambers should be addressed as there are slight discrepancies and problems associated with defining them within the pyramid.
Petrie describes the shafts of the Queen Chamber as rising into the pyramid after their short, horizontal straight lengths from within the chamber, at angles:
North Channel being an average of 37.4667º, where the western side of the shaft at first bend is 37.55º; middle of shaft is 37.4267º; eastern side of shaft is 37.4167º.
There can only be speculation as to why Petrie uses 37.4667º as the mean, considering 37.4833º would have been the mean.
South Channel being an average of 38.4667º, where western side is 38.4667º; middle is 38.33º; eastern side as 38.5833º.
Gantenbrink's Upuaut and the subsequent Upuaut 2 used in the shafts were able to survey the entirety of the shafts, and gave angles for them at their various bends throughout. The results for the south shaft are 39.6078º for its entire length of approximately 2,275" from the first bend once it leaves the chamber to its blocked end. The difference between the south shaft by both observations is 1.1411 degrees. A little more than one degree could have quite an effect upon the results of the analysis.
For the north shaft, Upuaut defined several angles to the shaft as it left the chamber and bent around the proximity of the gallery, but Gantenbrink provided nothing definite about where these angles lay within the shaft. Having a range between 33.3º and 40.1º could place the shaft anywhere on its rise through the pyramid, and as there is a difference between the two men for the south shaft, there could also be a difference between them for the first bend of the north shaft. According to Gantenbrink's diagrams of the shafts, the first angle is approximately 43º which is not included in his 'range'. There is another way to determine the north shaft, and that is by looking at the shafts of the King Chamber firstly.
Assessing the measurements for the King Chamber south shaft, we find Petrie has these, being taken from the outside down the shaft, and he does not have any angles from within the chamber:
At 0 to 120” from the surface: 45.4183º
At 120 to 240”: 45.5019º
At 240 to 360”: 45.4325º
At 360 to 480”: 45.4206º
At 480 to 600”: 45.2553º
At 600 to 720”: 45.1283º
At 720 to 840”: 44.4383º
Mean: 45.2278º as stated by Petrie, although the mean should be taken as 44.9701º.
Gantenbrink has the following observations, from inside the pyramid going outwards:
Start of bend: 39.2º
Next bend: 50.54º
Final bend and full length to exit: 45º
Gantenbrink provides the distance from within the chamber to the first bend, and with the angle there plus measurements and angles for the next bends and lengths, these can be modelled and laid out. Petrie states the position of the exit point upon the pyramid casing as being 3,148.95” above the pavement, in the 104th course if this were levelled out to the casing. Taking Gantenbrink’s figures places the exit point some 40-odd inches above the actual exit point, and this cannot do for the model’s exactness, let alone the pyramid itself. In using Gantenbrink’s initial angles and lengths of the shaft between these angles, the final angle leading to the casing would be 43.665º, not 45º. To use Petrie’s angles down to the 840” mark would mean an angle of 42º from that to Gantenbrink’s third angle, which is 3º difference. One possibility is to take the first bend beyond the chamber and link it to the exit point upon the proposed casing, and accept a complete angle of 44.052º, no matter the adjustments through the shaft itself. This can be called a 'true angle', and true angles could be applied to all the shafts in lieu of the various angles they contain.
For the north shaft, Petrie has measured from the outside coming down the shaft:
At 84 to 180": 32.079º
At 180 to 300": 31.621º
At 300 to 372": 30.721º
Mean: 31.55º as stated by Petrie, but the mean should be 31.4º.
Gantenbrink has more detailed angles going up the shaft, starting with the first angle after leaving the chamber at 17º, and after bending several times around the proximity of the gallery, ending with 32.6º for the last length to the exit. This is half a degree more than Petrie has for the final part of the shaft, and modelling this in the pyramid causes a problem with the exit upon the casing being some 60-odd inches above its actual exit point. Petrie has the measurement of 3,119.85” above the pavement for the exit point, being the base of the 103rd course if it were extended out to the casing. In consideration of the exit point upon the casing, the angle of 30.718º must be correct instead of 32.6º for the entire last length, despite what slight changes must exist.
Considering the north shaft of the Queen Chamber, and that there are several adjustments to the shaft going around the gallery, the most plausible operation is to consider the south shaft, and correct the angles appropriately towards an acceptable result. Final adjustments can be made once the correct astral overlay is found, and the true angles of the shafts can be understood. By choosing 'true angles', the better estimation for them would be to take the first bend in the shafts after they have left the chambers, and the end-positions of the shafts themselves, and define the angles they reveal.
For the King Chamber shafts, as we know their exit points upon the surface of the pyramid and the locations of the first bends from the chamber, the 'true angles' can be given as:
South shaft: 44.052º
North shaft: 30.945º
For the Queen Chamber shafts:
South shaft: 39.415º
North shaft: 40.2º
Again, these will rely on the correct astronomical overlay to confirm them, but certainly they will suffice despite the arguments for using the angles of either men implicitly.
The angle of the entrance passage - that which enters the pyramid and reaches the lower passage to the subterranean chamber - is 26.523º. The angle of the ascending passage - that which extends from the blocking plugs leading to the Grand Gallery - is 26.042º. For the Gallery itself, an angle of 26.278º is identified, and these angles are given by Petrie. The floor levels of the three chambers and their passages are from Petrie.
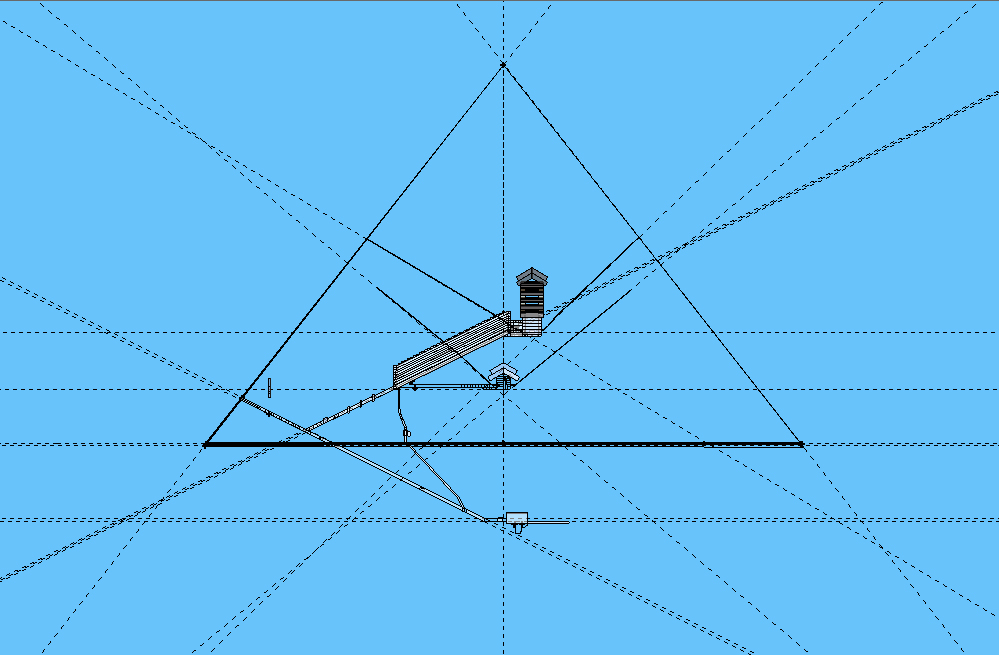
With these particulars, the model was constructed and accounted for with projections to the shaft angles and passage angles leading away from the pyramid; intersections were identified according to the heights of the shafts and passages and the potential of exacting intersection they had with each other, and also with extended alignments from such as floor levels. The following image is the reconstructed pyramid with projections of passages, shafts, and the floor levels of the two upper chambers, and floor and ceiling levels of the passage to the Subterranean Chamber.
It
can be seen that there are many intersections available for scrutiny,
but the problem is to identify a central position from which to
measure to the intersections in order to assess them. As can be seen
in the projection of the passages with dashed lines of their floors
and ceilings, such intersections are not a single figure but a range
between two figures, or a boundary band.
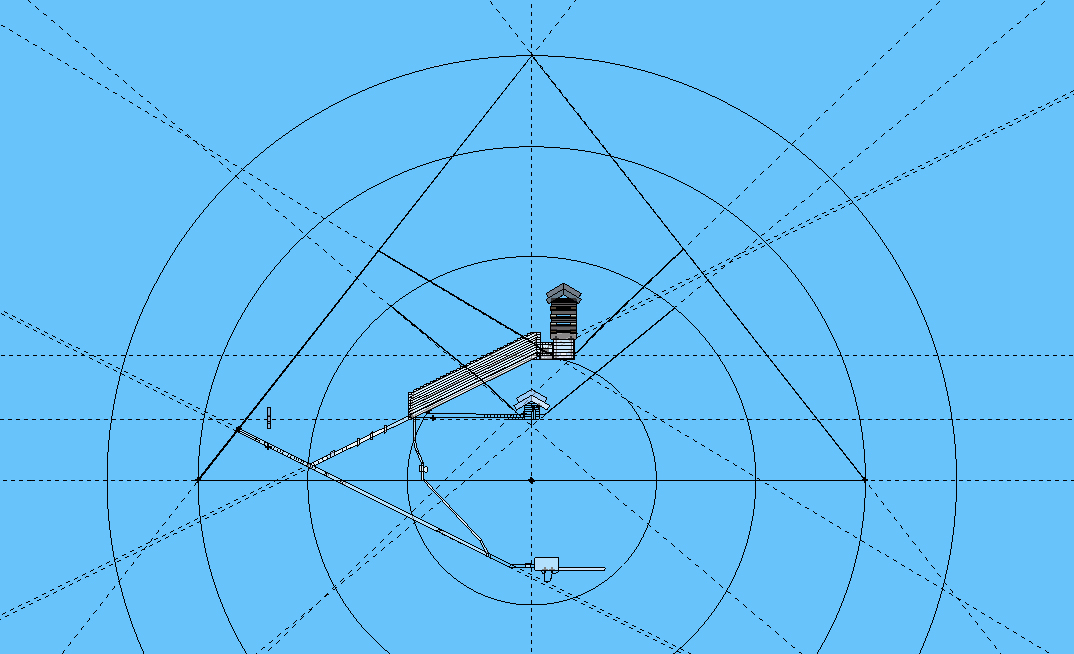
It is best to start with the pavement level for assessing associations between boundaries and particulars of the pyramid. We know the structure of the pyramid, and defining a centre-point from which to make measurements outwards gives us a firm basis, although it won't be necessary to measure out to all intersections like those in the image above, nor all parts of the pyramid such as the passage intersections or transition areas between passage and chamber, nor the end-points of the chambers. The following image shows four boundaries from the centre-point upon the pavement: to the apex; the base-side; the entrance and ascending passage's intersection; and the edge of the top step in the gallery.
What can be seen is these boundaries do not align with any intersections, although the intersection of the passages within the pyramid, specifically the centre of the ascending passage upon the floor of the entrance passage, does cast its boundary upon the the blocking stone of the niche at the top of the north shaft of the Queen Chamber, and the centre of the niche in the south shaft. In making boundaries to intersections of the projections, they are all individual measurements, with none aligning to two or more of those.
It is best to start with the pavement level for assessing associations between boundaries and particulars of the pyramid. We know the structure of the pyramid, and defining a centre-point from which to make measurements outwards gives us a firm basis, although it won't be necessary to measure out to all intersections like those in the image above, nor all parts of the pyramid such as the passage intersections or transition areas between passage and chamber, nor the end-points of the chambers. The following image shows four boundaries from the centre-point upon the pavement: to the apex; the base-side; the entrance and ascending passage's intersection; and the edge of the top step in the gallery.
What can be seen is these boundaries do not align with any intersections, although the intersection of the passages within the pyramid, specifically the centre of the ascending passage upon the floor of the entrance passage, does cast its boundary upon the the blocking stone of the niche at the top of the north shaft of the Queen Chamber, and the centre of the niche in the south shaft. In making boundaries to intersections of the projections, they are all individual measurements, with none aligning to two or more of those.
There
can be no doubt that the form of the pyramid is essential in its
measurements and placement of passages, chambers and shafts, and the
base of it certainly signifies an important interaction between the
pyramid itself and the plan it is based upon. That there may be
several layers of meaning for this plan may be reflected in there
being several levels from which to associate a proposed celestial
overlay to the architecture of the pyramid, based upon a centre-point
being upon each of the levels. While multiple levels means there are
multiple centre-points from which to cast boundaries, there would
only be one centre-point which truly ties together the essence of
this analysis, while other centre-points would show agreements and
cross-checks that celestial associations do exist within and of the
pyramid. In a later section is the inclusion of various levels and
centre-points, and how they solidify the entirety of this analysis,
but certainly seeking the all important centre-point is based upon
several necessities.
When the exact location for a centre point is found and boundaries and bands cast upon the pyramid, the observations of radius measurements to various intersections and particulars of the pyramid should offer up some exacting correlations between certain of them in some way. For example: the position of the entrance into the pyramid would be a certain measurement giving a radius of a circle overlaid upon the entire diagram, and apart from this circle including some other particular intersection with some other part of the pyramid and/or with some other intersection of projected alignments, the radius measure could also be found in another area of the pyramid in such as a particular course-height above the pavement and the measurement of that; or the width of that particular course-height from one side of the casing to the other. Of course, the boundary may also pass across a particular star or many stars, such is the purpose of defining an astronomical overlay that defines the planning period of the pyramid. Otherwise, the value of the measure might offer some significance for the value itself, possibly in relation to pi or the square root of a number, or in a relationship to some other measure.
The Queen’s Chamber has been identified as being an all important feature within the pyramid. Petrie gives two statements concerning the east-west axis of the ridge line of the roof being in the middle of the pyramid’s east-west axis: that it is; and that it is also possibly .3" south of that centre. A further observation concerning the top step of the Grand Gallery is that the face of this is possibly .4" south of the axis. Both of these locations and their measurements are carried by a discrepancy measurement of plus or minus .8" according to the central axis of the pyramid. For the purposes of being as exact as possible for the model, I will accept that both locations are centred upon the pyramid's east/west axis, and if there is need to adjust this it will be by only .05 of an inch at either location.
The floor level of the Queen Chamber is a particular height above the pavement, although the passage leading to this chamber has a step in it, giving the passage a double level. The step was made when in the mid 1800s, Howard Vyse lifted several floor stones in search of a hidden passage, starting at the chamber and working his way back to the gallery, stopping when he decided there most likely was not a hidden passage. In this light, the understanding of the passage to the chamber is that once it was accessed from the gallery, there was no hindrance to gaining the chamber, and that the floor was actually higher than the floor of the chamber, which meant there was a step down to entering the chamber from the passage.
While seeking a specific location that is to be used as a centre-point within the pyramid, from which to define boundaries and bands of intersections that this analysis will seek to uncover as being related to an astronomical overlay the pyramid is based upon, many possibilities were extensively tested before a definite position was identified, not upon the base of the pyramid but 105.05" below the floor of the Queen Chamber, on the join between the 20th and 21st courses, aligned upon the east/west axis of the pyramid . There could be good arguments for selecting any other location but the mathematics that arose because of this location made it impossible for any other spot to be accepted as better. This is true for the initial investigation, but as will be seen, there are other areas that can be used as a horizontal level for astronomical overlays as well as an alternative vertical axis.
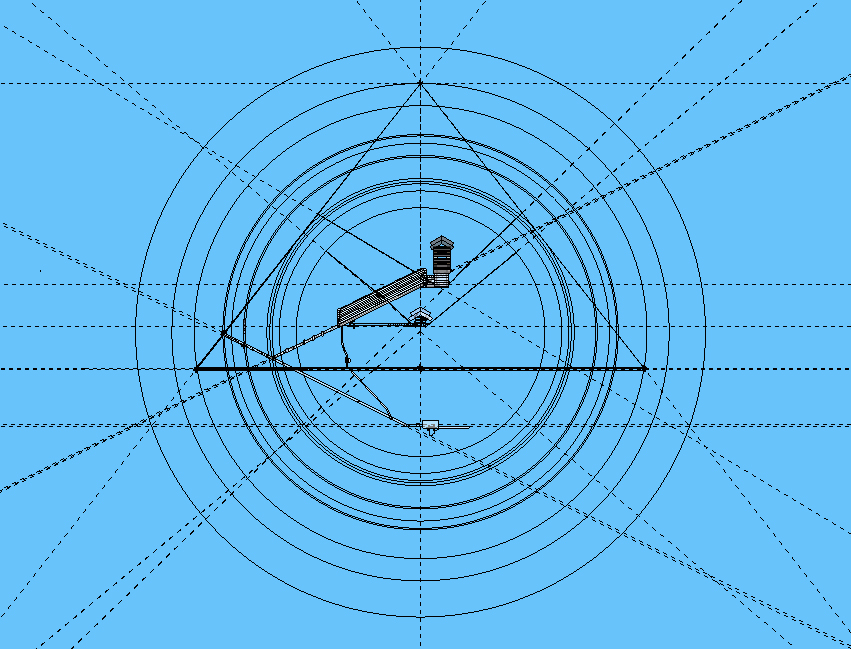
Initially, many possible intersections were identified and circular boundaries cast upon the model. Due to the heights of the shafts and passages, bands were made across some intersections because of the ranges given for these boundaries, while other intersections are upon single dashed lines. The following is a list of many possible boundaries and bands from the centre point beneath the Queen Chamber - from now on identified as C.P. - given in whole numbers rather than parts of an inch. It cannot be certain how many of these might be crucial to understanding the pyramid on some fundamental level, if any of them, but to list them and know them might come in handy.
Queen Chamber north shaft and descending passage: 7,650" - 7,870"
Entrance passage and floor level King chamber: 6,040" - 6,144"
Northern Shafts intersection: 6,020"
To apex of pyramid: 5,047"
To base of pyramid upon pavement, north/south axis: 4,596"
Entrance passage and floor level Queen chamber: 4,240" - 4,347"
Original entrance: 3,983" - 4,014"; centre of: 4,000"
Southern Shafts intersection: 3,755"
Entrance Glyph: 3,554" – 3,587"
Extension to closest estimated casing location: 3,119"
Entrance passage roof and Ascending passage: 3,012" - 3,060"
Proposed location of upper shaft's blocked cavities, centre of: 2,867"
Lower shaft's blocked cavities, centre of: 2,526"
Entrance passage juncture with Subterranean passage: 1,893" - 1,936"
Entrance within Subterranean chamber: 1,873" - 1,913"
Entrance to Grand Gallery on floor: 1,633"
Well shaft in Gallery: 1,585" - 1,609"
Edge of top step in Gallery: 962"
Entrance to King Chamber on floor: 1,019"
East/west apex of Queen Chamber roof: 350"
Inner roof join of top chamber: 1,848"
The apex of the gabled roof blocks in the top chamber has been estimated at 2,525" above the pavement by Colonel Howard Vyse who also surveyed the pyramid. Petrie did not argue this estimation.
The following image identifies many boundaries for the intersections mentioned above, but as the correct angles for the shafts are based upon 'true angles', there is still the possibility of either Petrie's or Gantenbrink's angles having some influence upon the intersection of the two northern shafts, and intersection of the two southern shafts. These two boundaries are particular radii right now, but adjustments could have them aligned with other measurements for other boundaries and a definite measurement selected, in so far as the radius to the closest casing point is within the band for the intersection for the descending and ascending passage's floor levels, and a certain radius chosen that defines some particular point in the intersection of the passages influences the location of the casing and a single boundary identifies the two points in one.
When the exact location for a centre point is found and boundaries and bands cast upon the pyramid, the observations of radius measurements to various intersections and particulars of the pyramid should offer up some exacting correlations between certain of them in some way. For example: the position of the entrance into the pyramid would be a certain measurement giving a radius of a circle overlaid upon the entire diagram, and apart from this circle including some other particular intersection with some other part of the pyramid and/or with some other intersection of projected alignments, the radius measure could also be found in another area of the pyramid in such as a particular course-height above the pavement and the measurement of that; or the width of that particular course-height from one side of the casing to the other. Of course, the boundary may also pass across a particular star or many stars, such is the purpose of defining an astronomical overlay that defines the planning period of the pyramid. Otherwise, the value of the measure might offer some significance for the value itself, possibly in relation to pi or the square root of a number, or in a relationship to some other measure.
The Queen’s Chamber has been identified as being an all important feature within the pyramid. Petrie gives two statements concerning the east-west axis of the ridge line of the roof being in the middle of the pyramid’s east-west axis: that it is; and that it is also possibly .3" south of that centre. A further observation concerning the top step of the Grand Gallery is that the face of this is possibly .4" south of the axis. Both of these locations and their measurements are carried by a discrepancy measurement of plus or minus .8" according to the central axis of the pyramid. For the purposes of being as exact as possible for the model, I will accept that both locations are centred upon the pyramid's east/west axis, and if there is need to adjust this it will be by only .05 of an inch at either location.
The floor level of the Queen Chamber is a particular height above the pavement, although the passage leading to this chamber has a step in it, giving the passage a double level. The step was made when in the mid 1800s, Howard Vyse lifted several floor stones in search of a hidden passage, starting at the chamber and working his way back to the gallery, stopping when he decided there most likely was not a hidden passage. In this light, the understanding of the passage to the chamber is that once it was accessed from the gallery, there was no hindrance to gaining the chamber, and that the floor was actually higher than the floor of the chamber, which meant there was a step down to entering the chamber from the passage.
While seeking a specific location that is to be used as a centre-point within the pyramid, from which to define boundaries and bands of intersections that this analysis will seek to uncover as being related to an astronomical overlay the pyramid is based upon, many possibilities were extensively tested before a definite position was identified, not upon the base of the pyramid but 105.05" below the floor of the Queen Chamber, on the join between the 20th and 21st courses, aligned upon the east/west axis of the pyramid . There could be good arguments for selecting any other location but the mathematics that arose because of this location made it impossible for any other spot to be accepted as better. This is true for the initial investigation, but as will be seen, there are other areas that can be used as a horizontal level for astronomical overlays as well as an alternative vertical axis.
Initially, many possible intersections were identified and circular boundaries cast upon the model. Due to the heights of the shafts and passages, bands were made across some intersections because of the ranges given for these boundaries, while other intersections are upon single dashed lines. The following is a list of many possible boundaries and bands from the centre point beneath the Queen Chamber - from now on identified as C.P. - given in whole numbers rather than parts of an inch. It cannot be certain how many of these might be crucial to understanding the pyramid on some fundamental level, if any of them, but to list them and know them might come in handy.
Queen Chamber north shaft and descending passage: 7,650" - 7,870"
Entrance passage and floor level King chamber: 6,040" - 6,144"
Northern Shafts intersection: 6,020"
To apex of pyramid: 5,047"
To base of pyramid upon pavement, north/south axis: 4,596"
Entrance passage and floor level Queen chamber: 4,240" - 4,347"
Original entrance: 3,983" - 4,014"; centre of: 4,000"
Southern Shafts intersection: 3,755"
Entrance Glyph: 3,554" – 3,587"
Extension to closest estimated casing location: 3,119"
Entrance passage roof and Ascending passage: 3,012" - 3,060"
Proposed location of upper shaft's blocked cavities, centre of: 2,867"
Lower shaft's blocked cavities, centre of: 2,526"
Entrance passage juncture with Subterranean passage: 1,893" - 1,936"
Entrance within Subterranean chamber: 1,873" - 1,913"
Entrance to Grand Gallery on floor: 1,633"
Well shaft in Gallery: 1,585" - 1,609"
Edge of top step in Gallery: 962"
Entrance to King Chamber on floor: 1,019"
East/west apex of Queen Chamber roof: 350"
Inner roof join of top chamber: 1,848"
The apex of the gabled roof blocks in the top chamber has been estimated at 2,525" above the pavement by Colonel Howard Vyse who also surveyed the pyramid. Petrie did not argue this estimation.
The following image identifies many boundaries for the intersections mentioned above, but as the correct angles for the shafts are based upon 'true angles', there is still the possibility of either Petrie's or Gantenbrink's angles having some influence upon the intersection of the two northern shafts, and intersection of the two southern shafts. These two boundaries are particular radii right now, but adjustments could have them aligned with other measurements for other boundaries and a definite measurement selected, in so far as the radius to the closest casing point is within the band for the intersection for the descending and ascending passage's floor levels, and a certain radius chosen that defines some particular point in the intersection of the passages influences the location of the casing and a single boundary identifies the two points in one.
This
image appears to have potential for any analysis into the pyramid,
and certainly there have been similar made when associations between
parts of the pyramid have been investigated, but none have defined
the relationship between the entrance glyph and the two small courses
of the 20th and 21st. In essence, I am stating that an association
between an astronomical overlay upon the pyramid has this level as
the most important horizon, and all overlays imaged will be aligned
by having the horizon line placed exactly along this level. In other
words, this level is one axis within the pyramid, used in conjunction
with the east/west axis of the pyramid which passes through the
centre of the Queen Chamber and across the face of the step in the
gallery.
While there are possible mathematical associations between these boundaries, if not singularly revealed by their own measurements, the main focus of this analysis is towards an astronomical reference, and this a more time consuming adventure than it first seemed like, as will be seen in the next section.
PREVIOUS
NEXT
INDEX
While there are possible mathematical associations between these boundaries, if not singularly revealed by their own measurements, the main focus of this analysis is towards an astronomical reference, and this a more time consuming adventure than it first seemed like, as will be seen in the next section.
PREVIOUS
NEXT
INDEX